Me 163B polars
Shown here is the polar as presented in 'Der Streng Geheime Vogel Me 163' by Wolfgang Späte, Appendix C, page 309-310. It is a combination of actual measurements (source yet unknown) and calculations. The calculations for Mach 0.5 to 0.8 were made according to a method presented in 'Aircraft performance, stability and control' by Perkins and Hage, Wiley, New York, 1963. The graph identifies the polars as approximations. The graph identifies CL=0.57 as the lift-off value.
According to the accompanying text, the basic polar (Mach below 0.5) is given by the standard equation CD = CD0 + CL^2 / (pi*A*e). CD0 is 0.013, aspect ratio 4.41, Oswald correction factor 0.786. The aspect ratio figure is based on wing surface figure of 19.6 m^2, while I keep measuring 17.4 m^2, using the standard definition of wing area of extending the leading and trailing edges to the centerline. Possibly the gross area (wing plus fuselage) is 19.6 m^2. Using a wing area figure of 17.4 m^2, I calculate an aspect ratio of 5.0.
Measurement of the data points and graphs below.
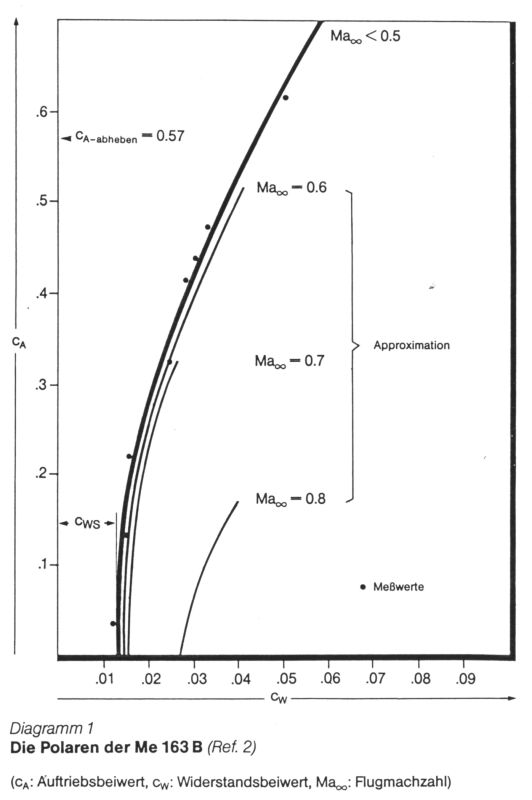
The data points were measured digitally.
| Drag coefficient | Lift coefficient |
| 0.0122 | 0.033 |
| 0.0151 | 0.131 |
| 0.0158 | 0.218 |
| 0.0248 | 0.321 |
| 0.0284 | 0.411 |
| 0.0305 | 0.435 |
| 0.0333 | 0.469 |
| 0.0505 | 0.611 |
The curves were measured and the equations below were the calculated as best fit equations.
| M<0.5 | CD = 0.0130 + 0.0953 * CL^2 |
| M=0.6 | CD = 0.0141 + 0.1037 * CL^2 |
| M=0.7 | CD = 0.0154 + 0.1015 * CL^2 |
| M=0.8 | CD = 0.0283 + 0.4473 * CL^2 |