| I've been studying the AQM-91 for a long time. The A&V scale model has wings with a strange profile, and I've long considered making new wing parts, preferably with 3D CAD and 3D printing. However I could not find information on the profiles used. Therefore I was happy to finally find a drawing that showed the wing and tail surfaces geometry, and the NACA profiles used. They are NACA 64A310 (mod), 64A306 (mod) and 64A007 (mod). For future 3D CAD work, I wanted to establish the profile coordinates. That turned out to be quite a bit of work and research, but I think the results are good. |
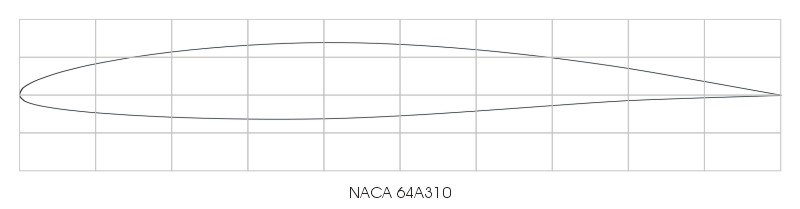
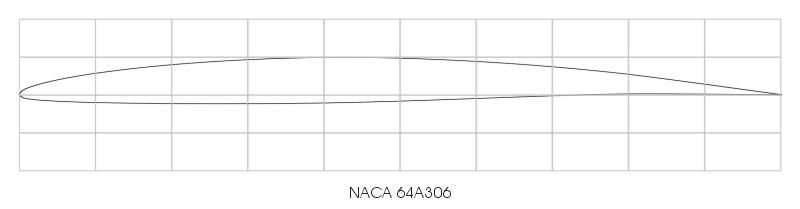
To start with the results: here are plots of the three profiles. The derivation and resulting coordinates are shown below.

The NACA 6-series airfoils were developed by means of conformal transformations, as described in NASA TM-4741 - Computer program to obtain ordinates for NACA airfoils and others references. I decided not to pursue this scientific way, but to use practical engineering approach instead, since this was more than adequate for the purpose. The webpage Thickness Function for NACA 6-Series Airfoils offers yet another method, but I did not use it either.
The coordinates for the (symmetrical) 64A006, 64A008 and 64A010 are taken from Abbott & Von Doenhoff, pages 354 to 356. Note that the footer on page 356 is not correct: it says 'NACA 643-018 Basic Thickness Distribution' but it is NACA 64A010. The NACA 6A-series airfoils have basically straight upper and lower lines aft of 80% chord, mostly for manufacturing reasons.
I checked whether the thickness distributions are simply scaled up, but the thickness ratios shows that there are small differences. The ratios also showed a peculiar ratio for 7.5 percent chord. A check in TN-1368 showed that the number 2.905 should be 2.805. The 64A007 data is linearly interpolated from 64A006 and 64A008, and thus the first result is found.
| 64A006 | 64A007 interpolated | 64A008 | 64A010 | ratio 006 vs 010 | ratio 008 vs 010 | |
| 0 | 0 | 0 | 0 | 0 | - | - |
| 0.5 | 0.485 | 0.566 | 0.646 | 0.804 | 0.603 | 0.803 |
| 0.75 | 0.585 | 0.682 | 0.778 | 0.969 | 0.604 | 0.803 |
| 1.25 | 0.739 | 0.861 | 0.983 | 1.225 | 0.603 | 0.802 |
| 2.5 | 1.016 | 1.185 | 1.353 | 1.688 | 0.602 | 0.802 |
| 5 | 1.399 | 1.631 | 1.863 | 2.327 | 0.601 | 0.801 |
| 7.5 | 1.684 | 1.965 | 2.245 | 2.905 (2.805) | 0.580 | 0.773 |
| 10 | 1.919 | 2.239 | 2.559 | 3.199 | 0.600 | 0.800 |
| 15 | 2.283 | 2.665 | 3.047 | 3.813 | 0.599 | 0.799 |
| 20 | 2.557 | 2.986 | 3.414 | 4.272 | 0.599 | 0.799 |
| 25 | 2.757 | 3.219 | 3.681 | 4.606 | 0.599 | 0.799 |
| 30 | 2.896 | 3.381 | 3.866 | 4.837 | 0.599 | 0.799 |
| 35 | 2.977 | 3.475 | 3.972 | 4.968 | 0.599 | 0.800 |
| 40 | 2.999 | 3.499 | 3.998 | 4.995 | 0.600 | 0.800 |
| 45 | 2.945 | 3.433 | 3.921 | 4.894 | 0.602 | 0.801 |
| 50 | 2.825 | 3.291 | 3.757 | 4.684 | 0.603 | 0.802 |
| 55 | 2.653 | 3.089 | 3.524 | 4.388 | 0.605 | 0.803 |
| 60 | 2.438 | 2.836 | 3.234 | 4.021 | 0.606 | 0.804 |
| 65 | 2.188 | 2.543 | 2.897 | 3.597 | 0.608 | 0.805 |
| 70 | 1.907 | 2.214 | 2.521 | 3.127 | 0.610 | 0.806 |
| 75 | 1.602 | 1.860 | 2.117 | 2.623 | 0.611 | 0.807 |
| 80 | 1.285 | 1.492 | 1.698 | 2.103 | 0.611 | 0.807 |
| 85 | 0.967 | 1.123 | 1.278 | 1.582 | 0.611 | 0.808 |
| 90 | 0.649 | 0.754 | 0.858 | 1.062 | 0.611 | 0.808 |
| 95 | 0.331 | 0.385 | 0.438 | 0.541 | 0.612 | 0.810 |
| 100 | 0.013 | 0.016 | 0.018 | 0.021 | - | - |
| LE radius | 0.246 | 0.343 | 0.439 | 0.687 | 0.358 | 0.639 |
I was puzzled by the question what camber line was used for the 64A family. Abbott & Von Doenhoff page 121 says: "When the mean-line designation is not given, it is understood that the uniform-load mean line (a=1.0) has been used". But the coordinates that I calculated with a = 1.0 did not match the NACA 64A210 and 64A410 data listed on pages 430 and 431. I then found the following in NACA TN-1368, page 2: 'A special mean line, designated the a = 0.8 (modified) mean line, has also been designed to maintain straight sides on the cambered sections". This indeed gave me matching coordinate data. One question remains for me: the a = 0.8 (modified) mean line is not perfectly straight for the last 20% chord, which is the whole idea behind the 6A series. The data below for the a = 0.8, a = 0.8 (modified) and a = 1.0 camber lines is taken from Abbott & Von Doenhoff, pages p402, 403 and 405. They represent the camber line for a design CL = 1, and are to be scaled according to the actual design CL.
| a=0.8 | a=0.8 mod | a=1.0 | ||||
| yc | dy/dx | yc | dy/dx | yc | dy/dx | |
| 0 | 0 | 0 | 0 | 0 | ||
| 0.5 | 0.287 | 0.48535 | 0.281 | 0.47539 | 0.250 | 0.42120 |
| 0.75 | 0.404 | 0.44925 | 0.396 | 0.44004 | 0.350 | 0.38875 |
| 1.25 | 0.616 | 0.40359 | 0.603 | 0.39531 | 0.535 | 0.34770 |
| 2.5 | 1.077 | 0.34104 | 1.055 | 0.33404 | 0.930 | 0.29155 |
| 5 | 1.841 | 0.27718 | 1.803 | 0.27149 | 1.580 | 0.23430 |
| 7.5 | 2.483 | 0.23868 | 2.432 | 0.23378 | 2.120 | 0.19995 |
| 10 | 3.043 | 0.2105 | 2.981 | 0.20618 | 2.585 | 0.17485 |
| 15 | 3.985 | 0.16892 | 3.903 | 0.16546 | 3.365 | 0.13805 |
| 20 | 4.748 | 0.13734 | 4.651 | 0.13452 | 3.980 | 0.11030 |
| 25 | 5.367 | 0.11101 | 5.257 | 0.10873 | 4.475 | 0.08745 |
| 30 | 5.863 | 0.08775 | 5.742 | 0.08595 | 4.860 | 0.06745 |
| 35 | 6.248 | 0.06634 | 6.120 | 0.06498 | 5.150 | 0.04925 |
| 40 | 6.528 | 0.04601 | 6.394 | 0.04507 | 5.355 | 0.03225 |
| 45 | 6.709 | 0.02613 | 6.571 | 0.02559 | 5.475 | 0.01595 |
| 50 | 6.790 | 0.00620 | 6.651 | 0.00607 | 5.515 | 0 |
| 55 | 6.770 | -0.01433 | 6.631 | -0.01404 | 5.475 | -0.01595 |
| 60 | 6.644 | -0.03611 | 6.508 | -0.03537 | 5.355 | -0.03225 |
| 65 | 6.405 | -0.06010 | 6.274 | -0.05887 | 5.150 | -0.04925 |
| 70 | 6.037 | -0.0879 | 5.913 | -0.0861 | 4.860 | -0.06745 |
| 75 | 5.514 | -0.12311 | 5.401 | -0.12058 | 4.475 | -0.08745 |
| 80 | 4.771 | -0.18412 | 4.673 | -0.18034 | 3.980 | -0.11030 |
| 85 | 3.683 | -0.23921 | 3.607 | -0.23430 | 3.365 | -0.13805 |
| 90 | 2.435 | -0.25583 | 2.452 | -0.24521 | 2.585 | -0.17485 |
| 95 | 1.163 | -0.24904 | 1.226 | -0.24521 | 1.58 | -0.23430 |
| 100 | 0 | -0.20385 | 0 | -0.24521 | 0 | |
To check my method, I had just one reference profile: the NACA 64A410 coordinates as listed on page 431 of Abbott & Von Doenhoff. I calculated 'my' 64A410 profile coordinates using the NACA 64A010 thickness distribution, combined with the a = 0.8 (modified) camber line scaled down to 40%, using the equations on page 113 of Abbott & Von Doenhoff.
I'm happy to report that the differences were very small. They are most likely rounding errors, slide rule vs computer. The large differences for 7.5% chord are again the result of the 2.805 vs 2.905 error, as reported above.
| 64A010 | a=0.8 mod | a=0.8 mod (40%) | 64A410 calculated | 64A410 A & vD p431 | deltas | |||||||||||||||||
| x | y | y | dy/dx | y | dy/dx | x upper | y upper | x lower | y lower | x upper | y upper | x lower | y lower | |||||||||
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||||
| 0.5 | 0.804 | 0.281 | 0.47539 | 0.112 | 0.190 | 0.350 | 0.902 | 0.650 | -0.677 | 0.350 | 0.902 | 0.650 | -0.678 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 0.75 | 0.969 | 0.396 | 0.44004 | 0.158 | 0.176 | 0.582 | 1.113 | 0.918 | -0.796 | 0.582 | 1.112 | 0.918 | -0.796 | 0.000 | 0.001 | 0.000 | 0.000 | |||||
| 1.25 | 1.225 | 0.603 | 0.39531 | 0.241 | 0.158 | 1.059 | 1.451 | 1.441 | -0.969 | 1.059 | 1.451 | 1.441 | -0.969 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 2.5 | 1.688 | 1.055 | 0.33404 | 0.422 | 0.134 | 2.276 | 2.095 | 2.724 | -1.251 | 2.276 | 2.095 | 2.724 | -1.251 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 5 | 2.327 | 1.803 | 0.27149 | 0.721 | 0.109 | 4.749 | 3.035 | 5.251 | -1.592 | 4.749 | 3.034 | 5.251 | -1.592 | 0.000 | 0.001 | 0.000 | 0.000 | |||||
| 7.5 | 2.805 | 2.432 | 0.23378 | 0.973 | 0.094 | 7.239 | 3.766 | 7.761 | -1.820 | 7.230 | 3.865 | 7.770 | -1.919 | 0.009 | -0.099 | -0.009 | 0.099 | |||||
| 10 | 3.199 | 2.981 | 0.20618 | 1.192 | 0.082 | 9.737 | 4.381 | 10.263 | -1.996 | 9.737 | 4.380 | 10.263 | -1.996 | 0.000 | 0.001 | 0.000 | 0.000 | |||||
| 15 | 3.813 | 3.903 | 0.16546 | 1.561 | 0.066 | 14.748 | 5.366 | 15.252 | -2.243 | 14.748 | 5.366 | 15.252 | -2.244 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 20 | 4.272 | 4.651 | 0.13452 | 1.860 | 0.054 | 19.770 | 6.126 | 20.230 | -2.405 | 19.770 | 6.126 | 20.230 | -2.406 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 25 | 4.606 | 5.257 | 0.10873 | 2.103 | 0.043 | 24.800 | 6.704 | 25.200 | -2.499 | 24.800 | 6.705 | 25.200 | -2.499 | 0.000 | -0.001 | 0.000 | 0.000 | |||||
| 30 | 4.837 | 5.742 | 0.08595 | 2.297 | 0.034 | 29.834 | 7.131 | 30.166 | -2.537 | 29.834 | 7.131 | 30.166 | -2.537 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 35 | 4.968 | 6.12 | 0.06498 | 2.448 | 0.026 | 34.871 | 7.414 | 35.129 | -2.518 | 34.871 | 7.414 | 35.129 | -2.518 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 40 | 4.995 | 6.394 | 0.04507 | 2.558 | 0.018 | 39.910 | 7.552 | 40.090 | -2.437 | 39.910 | 7.552 | 40.090 | -2.436 | 0.000 | 0.000 | 0.000 | -0.001 | |||||
| 45 | 4.894 | 6.571 | 0.02559 | 2.628 | 0.010 | 44.950 | 7.522 | 45.050 | -2.265 | 44.950 | 7.522 | 45.050 | -2.266 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 50 | 4.684 | 6.651 | 0.00607 | 2.660 | 0.002 | 49.989 | 7.344 | 50.011 | -2.024 | 49.989 | 7.344 | 50.011 | -2.024 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 55 | 4.388 | 6.631 | -0.01404 | 2.652 | -0.006 | 55.025 | 7.040 | 54.975 | -1.736 | 55.025 | 7.040 | 54.975 | -1.736 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 60 | 4.021 | 6.508 | -0.03537 | 2.603 | -0.014 | 60.057 | 6.624 | 59.943 | -1.417 | 60.057 | 6.624 | 59.943 | -1.418 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 65 | 3.597 | 6.274 | -0.05887 | 2.510 | -0.024 | 65.085 | 6.106 | 64.915 | -1.086 | 65.085 | 6.106 | 64.915 | -1.086 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 70 | 3.127 | 5.913 | -0.0861 | 2.365 | -0.034 | 70.108 | 5.490 | 69.892 | -0.760 | 70.108 | 5.490 | 69.892 | -0.760 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 75 | 2.623 | 5.401 | -0.12058 | 2.160 | -0.048 | 75.126 | 4.780 | 74.874 | -0.460 | 75.126 | 4.780 | 74.874 | -0.460 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 80 | 2.103 | 4.673 | -0.18034 | 1.869 | -0.072 | 80.151 | 3.967 | 79.849 | -0.228 | 80.151 | 3.967 | 79.849 | -0.229 | 0.000 | 0.000 | 0.000 | 0.001 | |||||
| 85 | 1.582 | 3.607 | -0.2343 | 1.443 | -0.094 | 85.148 | 3.018 | 84.852 | -0.132 | 85.148 | 3.018 | 84.852 | -0.132 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 90 | 1.062 | 2.452 | -0.24521 | 0.981 | -0.098 | 90.104 | 2.038 | 89.896 | -0.076 | 90.104 | 2.038 | 89.896 | -0.076 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 95 | 0.541 | 1.226 | -0.24521 | 0.490 | -0.098 | 95.053 | 1.029 | 94.947 | -0.048 | 95.053 | 1.028 | 94.947 | -0.048 | 0.000 | 0.001 | 0.000 | 0.000 | |||||
| 100 | 0.021 | 0 | -0.24521 | 0.000 | -0.098 | 100.002 | 0.021 | 99.998 | -0.021 | 100.000 | 0.021 | 100.000 | -0.021 | 0.002 | 0.000 | -0.002 | 0.000 | |||||
Now the method has been verified, NACA 64A306 profile coordinates were calculated using the NACA 64A006 thickness distribution, combined with the a = 0.8 (modified) camber line scaled down to 30%.
| 64A006 | a=0.8 mod | a=0.8 mod (30%) | 64A306 calculated | |||||||||
| x | y | y | dy/dx | y | dy/dx | x upper | y upper | x lower | y lower | |||
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 0.5 | 0.485 | 0.281 | 0.47539 | 0.084 | 0.143 | 0.432 | 0.564 | 0.568 | -0.396 | |||
| 0.75 | 0.585 | 0.396 | 0.44004 | 0.119 | 0.132 | 0.673 | 0.699 | 0.827 | -0.461 | |||
| 1.25 | 0.739 | 0.603 | 0.39531 | 0.181 | 0.119 | 1.163 | 0.915 | 1.337 | -0.553 | |||
| 2.5 | 1.016 | 1.055 | 0.33404 | 0.317 | 0.100 | 2.399 | 1.327 | 2.601 | -0.694 | |||
| 5 | 1.399 | 1.803 | 0.27149 | 0.541 | 0.081 | 4.886 | 1.935 | 5.114 | -0.853 | |||
| 7.5 | 1.684 | 2.432 | 0.23378 | 0.730 | 0.070 | 7.382 | 2.409 | 7.618 | -0.950 | |||
| 10 | 1.919 | 2.981 | 0.20618 | 0.894 | 0.062 | 9.882 | 2.810 | 10.118 | -1.021 | |||
| 15 | 2.283 | 3.903 | 0.16546 | 1.171 | 0.050 | 14.887 | 3.451 | 15.113 | -1.109 | |||
| 20 | 2.557 | 4.651 | 0.13452 | 1.395 | 0.040 | 19.897 | 3.950 | 20.103 | -1.160 | |||
| 25 | 2.757 | 5.257 | 0.10873 | 1.577 | 0.033 | 24.910 | 4.333 | 25.090 | -1.178 | |||
| 30 | 2.896 | 5.742 | 0.08595 | 1.723 | 0.026 | 29.925 | 4.618 | 30.075 | -1.172 | |||
| 35 | 2.977 | 6.12 | 0.06498 | 1.836 | 0.019 | 34.942 | 4.812 | 35.058 | -1.140 | |||
| 40 | 2.999 | 6.394 | 0.04507 | 1.918 | 0.014 | 39.959 | 4.917 | 40.041 | -1.081 | |||
| 45 | 2.945 | 6.571 | 0.02559 | 1.971 | 0.008 | 44.977 | 4.916 | 45.023 | -0.974 | |||
| 50 | 2.825 | 6.651 | 0.00607 | 1.995 | 0.002 | 49.995 | 4.820 | 50.005 | -0.830 | |||
| 55 | 2.653 | 6.631 | -0.01404 | 1.989 | -0.004 | 55.011 | 4.642 | 54.989 | -0.664 | |||
| 60 | 2.438 | 6.508 | -0.03537 | 1.952 | -0.011 | 60.026 | 4.390 | 59.974 | -0.485 | |||
| 65 | 2.188 | 6.274 | -0.05887 | 1.882 | -0.018 | 65.039 | 4.070 | 64.961 | -0.305 | |||
| 70 | 1.907 | 5.913 | -0.0861 | 1.774 | -0.026 | 70.049 | 3.680 | 69.951 | -0.132 | |||
| 75 | 1.602 | 5.401 | -0.12058 | 1.620 | -0.036 | 75.058 | 3.221 | 74.942 | 0.019 | |||
| 80 | 1.285 | 4.673 | -0.18034 | 1.402 | -0.054 | 80.069 | 2.685 | 79.931 | 0.119 | |||
| 85 | 0.967 | 3.607 | -0.2343 | 1.082 | -0.070 | 85.068 | 2.047 | 84.932 | 0.117 | |||
| 90 | 0.649 | 2.452 | -0.24521 | 0.736 | -0.074 | 90.048 | 1.383 | 89.952 | 0.088 | |||
| 95 | 0.331 | 1.226 | -0.24521 | 0.368 | -0.074 | 95.024 | 0.698 | 94.976 | 0.038 | |||
| 100 | 0.013 | 0 | -0.24521 | 0.000 | -0.074 | 100.001 | 0.013 | 99.999 | -0.013 | |||
NACA 64A310 profile coordinates were calculated using the NACA 64A010 thickness distribution, combined with the a = 0.8 (modified) camber line scaled down to 30%.
| 64A010 | a=0.8 mod | a=0.8 mod (30%) | 64A310 calculated | |||||||||
| x | y | y | dy/dx | y | dy/dx | x upper | y upper | x lower | y lower | |||
| 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 0.5 | 0.804 | 0.281 | 0.47539 | 0.084 | 0.143 | 0.386 | 0.880 | 0.614 | -0.712 | |||
| 0.75 | 0.969 | 0.396 | 0.44004 | 0.119 | 0.132 | 0.623 | 1.079 | 0.877 | -0.842 | |||
| 1.25 | 1.225 | 0.603 | 0.39531 | 0.181 | 0.119 | 1.106 | 1.397 | 1.394 | -1.036 | |||
| 2.5 | 1.688 | 1.055 | 0.33404 | 0.317 | 0.100 | 2.332 | 1.996 | 2.668 | -1.363 | |||
| 5 | 2.327 | 1.803 | 0.27149 | 0.541 | 0.081 | 4.811 | 2.860 | 5.189 | -1.778 | |||
| 7.5 | 2.805 | 2.432 | 0.23378 | 0.730 | 0.070 | 7.304 | 3.528 | 7.696 | -2.069 | |||
| 10 | 3.199 | 2.981 | 0.20618 | 0.894 | 0.062 | 9.803 | 4.087 | 10.197 | -2.299 | |||
| 15 | 3.813 | 3.903 | 0.16546 | 1.171 | 0.050 | 14.811 | 4.979 | 15.189 | -2.637 | |||
| 20 | 4.272 | 4.651 | 0.13452 | 1.395 | 0.040 | 19.828 | 5.664 | 20.172 | -2.873 | |||
| 25 | 4.606 | 5.257 | 0.10873 | 1.577 | 0.033 | 24.850 | 6.181 | 25.150 | -3.026 | |||
| 30 | 4.837 | 5.742 | 0.08595 | 1.723 | 0.026 | 29.875 | 6.558 | 30.125 | -3.113 | |||
| 35 | 4.968 | 6.12 | 0.06498 | 1.836 | 0.019 | 34.903 | 6.803 | 35.097 | -3.131 | |||
| 40 | 4.995 | 6.394 | 0.04507 | 1.918 | 0.014 | 39.932 | 6.913 | 40.068 | -3.076 | |||
| 45 | 4.894 | 6.571 | 0.02559 | 1.971 | 0.008 | 44.962 | 6.865 | 45.038 | -2.923 | |||
| 50 | 4.684 | 6.651 | 0.00607 | 1.995 | 0.002 | 49.991 | 6.679 | 50.009 | -2.689 | |||
| 55 | 4.388 | 6.631 | -0.01404 | 1.989 | -0.004 | 55.018 | 6.377 | 54.982 | -2.399 | |||
| 60 | 4.021 | 6.508 | -0.03537 | 1.952 | -0.011 | 60.043 | 5.973 | 59.957 | -2.068 | |||
| 65 | 3.597 | 6.274 | -0.05887 | 1.882 | -0.018 | 65.064 | 5.479 | 64.936 | -1.714 | |||
| 70 | 3.127 | 5.913 | -0.0861 | 1.774 | -0.026 | 70.081 | 4.900 | 69.919 | -1.352 | |||
| 75 | 2.623 | 5.401 | -0.12058 | 1.620 | -0.036 | 75.095 | 4.242 | 74.905 | -1.001 | |||
| 80 | 2.103 | 4.673 | -0.18034 | 1.402 | -0.054 | 80.114 | 3.502 | 79.886 | -0.698 | |||
| 85 | 1.582 | 3.607 | -0.2343 | 1.082 | -0.070 | 85.111 | 2.660 | 84.889 | -0.496 | |||
| 90 | 1.062 | 2.452 | -0.24521 | 0.736 | -0.074 | 90.078 | 1.795 | 89.922 | -0.324 | |||
| 95 | 0.541 | 1.226 | -0.24521 | 0.368 | -0.074 | 95.040 | 0.907 | 94.960 | -0.172 | |||
| 100 | 0.021 | 0 | -0.24521 | 0.000 | -0.074 | 100.002 | 0.021 | 99.998 | -0.021 | |||